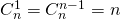Thuật toán tính tổ hợp – Cách tính tổ hợp trong C++

Trong Toán học, tổ hợp là cách chọn những phần tử từ một nhóm lớn hơn mà không phân biệt thứ tự. Ví dụ chọn 2 trong 3 phần tử {1, 2, 3 } sẽ có ba cách chọn đó là: {1, 2}, {1, 3}, {2, 3}.
Cách tính tổ hợp trong c++ bằng đệ quy
Ta có công thức truy hồi như sau: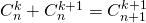
Với các tính chất sau:
Từ công thức truy hồi trên ta sẽ dễ dàng viết được một hàm đệ quy để tính tổ hợp như sau:
|
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
#include<iostream>
using namespace std;
int C(int k, int n) {
if (k == 0 || k == n) return 1;
if (k == 1) return n;
return C(k - 1, n - 1) + C(k, n - 1);
}
int main(){
int n, k;
cout << "Nhap k: ";
cin >> k;
cout << "Nhap n: ";
cin >> n;
cout << "To hop bang: " << C(k, n);
system("pause");
return 0;
}
|
Sau khi chạy chương trình thì chúng ta sẽ có kết quả sau
|
0
1
2
3
4
|
Nhap k: 3
Nhap n: 5
To hop bang: 10
|
Các bạn có thể thấy ở trên mình dùng ba điểm neo để làm điều kiện dừng đó là:
- Tại k bằng 0 hoặc k bằng n thì ta phải return 1
- Tại k bằng 1 thì ta return n
Hoàn toàn đúng với các tính chất mình đã trình bày ở trên nhé ^_^
Nhưng nhược điểm của phương pháp đệ quy này lại là tốc độ. không tin thì bạn cứ thử nhập k và n lớn xí nhé !
Cách tính tổ hợp trong c++ bằng phương pháp lặp
Số các tổ hợp chập k của n phần tử:
Với công thức trên thì ta chỉ cần viết một hàm tính giai thừa là xong rồi phải không nào. Chúng ta cùng bắt đầu nhé
|
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
#include<iostream>
using namespace std;
long long gt(int n) {
long long s = 1;
for (int i = 1; i <= n; i++)
s *= i;
return s;
}
long long C(int k, int n) {
return gt(n) / (gt(k)*gt(n - k));
}
int main(){
int n, k;
cout << "Nhap k: ";
cin >> k;
cout << "Nhap n: ";
cin >> n;
cout << "To hop bang: " << C(k, n);
system("pause");
return 0;
}
|
Mặc dù là nhanh nhưng cách làm trên vẫn không thể tính được nhũng số tổ hợp lớn được. Lý do đơn giản là vì khi tính ra giai thừa thì con số đã rất lớn.
Đam mê không phải là thứ có thể đến với bạn, cũng không phải là thứ bạn có thể nghĩ ra, mà đam mê là điều bạn phải dấn thân, tìm kiếm và quan trọng hơn hết là lựa chọn cho mình.
H.wiki mong muốn luôn cập nhật những thông tin hay và hữu ích cho tất cả mọi người.
Nếu bạn thấy bài viết này hay thì hãy like, chia sẻ với bạn bè, người thân và đừng quên ủng hộ blog nhé !